深度学习入门
前言
问题引入
想想一下,你正在研究一款新药,不妨为它起一个名字就叫“新-二甲双胍”。在药物的研制过程中,你想研究一些药物的摄入量和其药效之间的关系;为了简单起见,你把药物的服用的质量-体重比(g/kg)作为其摄入量;把服药后1h的血糖(mmol/L)作为药效的衡量指标;并且认为0.45-0.50mmol/L属于正常范围。
随后,你开展了一系列实验得到了下面这张图:
自然的,会希望使用某一种解析式来描述这个曲线;而且进一步的会希望使用最少的参数就能确定这个曲线。一个简单的想法是使用分段的线性拟合,其效果大约像这样:

很显然,这样的方法虽然使用的参数比较少,但是需要确定拐点,也就是实现不同线性函数之间的切换,这似乎不是一件容易的的事情。
当然了,我们也可以使用伟大的多项式拟合但是这种方法其实也不是很好,如果有做过大雾实验就这知道这种方法比较容易过拟合,也就是在某些点总是得到不很好的拟合。如果在低维中就出现了这种问题,自然不能指望在高维中也有很好的效果。
这里仅仅是顺戈一击,不要太在意
但是,如果有方法可以自动地帮助线性函数变弯;那么,使用线性函数的拟合,就是一个好主意了。幸运的是,这不是什么困难的事情!
这里的“变弯”仅仅是一种“图像”上的说法,更合适的说法是,调节不同的线性函数在不同范围上的对“总和”的贡献的大小。
拟合曲线
事实上,仅仅需要一些简单的线性函数和非线性函数,我们就可以很轻松的实现对这个曲线的拟合,如下图所示:

这里的蓝色和红色分布表示一个线性变化和一个非线性变化,我们是通过对应的线性函数和非线性函数实现的这种变化;特别的是,这里使用的非线性函数是一个sigmoid函数。这里我没有标注每一个线性变化中的参数,因为具体的参数是什么在这里并不重要,我们只要能从图中的纵坐标的变化上是可以看出对应的线性变化的发生就可以了。
需要指出的是,这里的sigmoid函数的形式是:$\sigma(x) = \frac{1}{1 + \mathrm{e}^{-x}}$,也就是说,它的参数都是固定的、已知的。而线性函数:$y = \mathrm{w} \cdot x + \mathrm{b}$中的$\mathrm{w}$和$\mathrm{b}$则是不知道的,是需要确定的。
这里,我们先不考虑这里的$\mathrm{w}$和$\mathrm{b}$是怎么确定的,而是深入的考察一下上图到底在干啥,这样的一个拟合的过程要怎么理解。
抽象化
这里是为了后面讨论的方法,主要是为了引入张量这件事
神经网络与曲线拟合
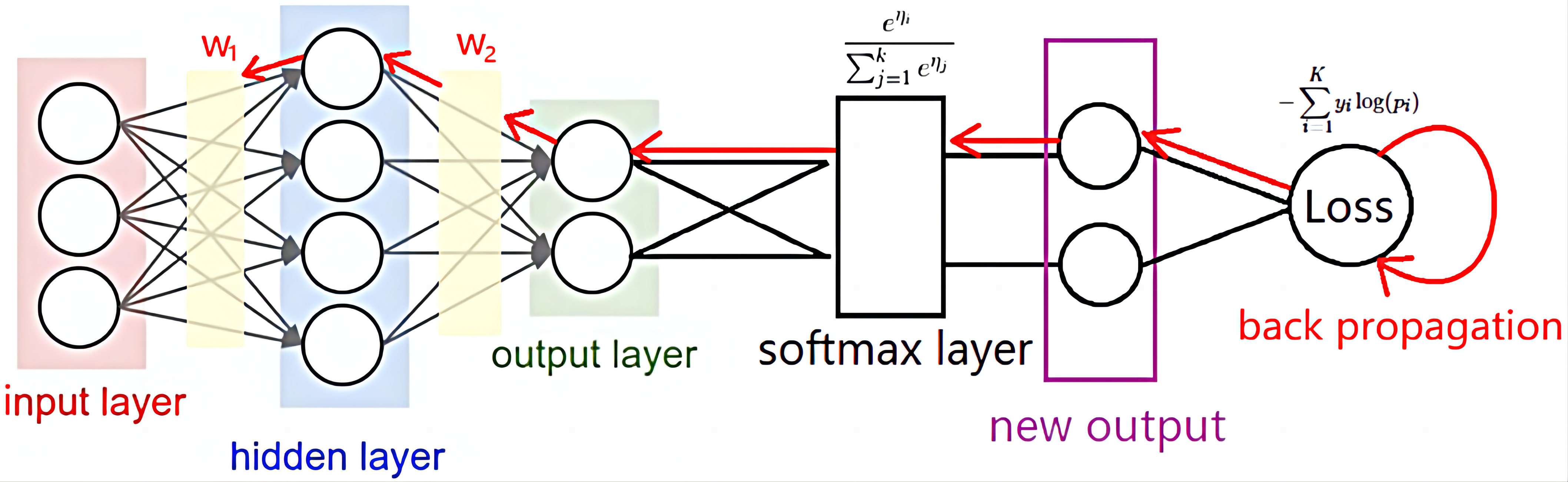
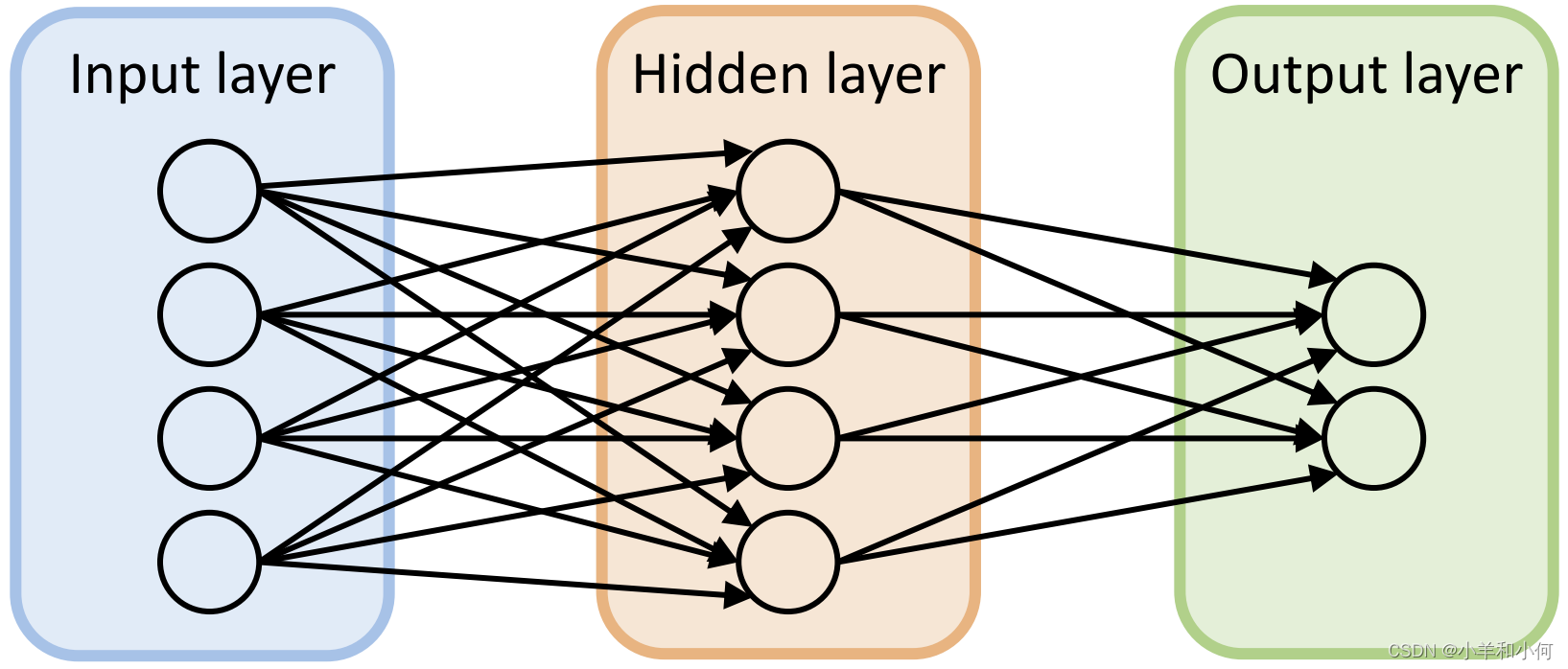
正如我们上文讨论的那样,对一个曲线的拟合事实上可以通过一些线性运算和非线性运算的叠加。而神经网络中所发生的就是这样的运算,如下图所示:
这里是强调forward中发生的事情,backward先不着急 >︿<

这里给出了一个简单的神经网络SimpleMLP,其内部结构事实上就是两个线性层,fc1和fc2,两个非线层,sigmoid1和softmax,一起形成的。输入的数据会依次经过:fc1>sigmoid1>fc2>softmax,得到最后的输出。
这就是多层感知机MLP的基本结构,而MLP是现代神经网络的最基本的形式。
这里,我们不妨先把这个fc1>sigmoid1>fc2>softmax的过程视作“某种变化”,也就是“一个黑箱”,我们只要输入一系列的数据,就能得到一系列的输出,而得到的输出正好和现实中的结果对的上号!如下图所示:

这里仅仅是用作示意,不要真的去观察箭头和数字是不是对的上哦🤣
所以,我们到这里就知道了,我们事实上可以把一个神经网络看作一系列线性函数和非线性函数逐次作用的结果。但是,总是使用这样的语言来描述一个神经网络总是不方法的,特别是,在研究网络优化和复杂网络上。所以下面我们希望引入一种更加抽象、通用的方法来描述其中发生的事情。
神经网络与张量
标量是零维的张量、向量/矢量是一维的张量、矩阵是二维的张量;这里指出,是希望下文不会引发什么歧义
线性代数教会我们的一个重要的事情就是:一个线性变化,可以用一个矩阵运算来表示,我们在学习的过程中经常干的一件事情就是用输入的向量和输出的向量来确定中间的转化矩阵。那么,如果我们先忽略神经网络中的那些非线性的部分,我们就会意识到,它们是一回事情。也就是说,我们可以用张量之间的运算代替神经网络中的线性部分的运算。
这里使用张量,是因为虽然我们学习线性代数时候总是见到向量和矩阵上的运算,但是现实中的数据总是高维的,比如图片,不用张量就难以描述。而且张量的运算的规律和它们是一样的。
那么非线性的部分要怎么解决呢?其实也很简单,我们使用逐元素的运算就可以了,所以,非线性运算就是对张量进行逐元素的运算;特别的,这里的元素应该是一个单射,也就是一个输入只能有一个唯一的输出。
希望下面这张图可以帮助你理解这个过程:

这里,我们把原本的线性运算使用张量之间的点乘代替;把原本的非线性运算用对张量的逐元素运算代替。解释了如何从输入$\mathbf{\vec{x^0}} \in \mathbb{R}^n$得到对应的预测$\mathbf{\vec{y^0}} \in \mathbb{R}^m$
值得注意的是,对一个神经网络可以有多个输入以及多个输出,而每一个输入或者输出可以是高维的信息(这往往意味着一个很长的向量)。
小结
综上所述,我们知道了神经网络在一定程度上和曲线拟合是一回事情;并且为了更好的描述其中的过程,也是为了应对高维和复杂网络的挑战,我们使用张量的语言来描述神经网络中的运算。这样一来,我们就已经描述了一个神经网络的forward也就是正向传播的过程。
但是,我们还没有解释神经网络中的那些未知的线性运算的参数,也就是那些张量$\mathbf{W}$和$\mathbf{b}$是怎么确定的。因为它们显然是经过仔细选择的,不然的话,预测得到的曲线怎么会和真实的曲线一致。而这些就是反向传播(backward)的过程了。
而且,我们还应该认识到,虽然我在这里给出的“引子”的输入是一个标量,但是事实上的输入是一个张量。也就是说,它是一个高维的信息,比如说一个512*512的RGB图像,它里面就有262114个像素而每一个像素有3个数字控制对应的三通道的值,也就是说,为了完整的描述这个图像应该需要786432个参数。而这仅仅是一个图像而已,现实中的图像更是数以亿计。
这样一来,考虑到线性方程求解的时候的要求,我们的网络也会需要大量的参数,也就是那些$\mathbf{W}$和$\mathbf{b}$。这样,如何高效的优化这些参数,使得它们可以很好的捕捉输入和输出之间的关系,就是紧要之处了。
而backward正是对这个问题的回答!